알고리즘/Baekjoon
[PS] 세미나 배정 / C++ (백준 28305번)
dh_0e
2024. 8. 19. 21:09
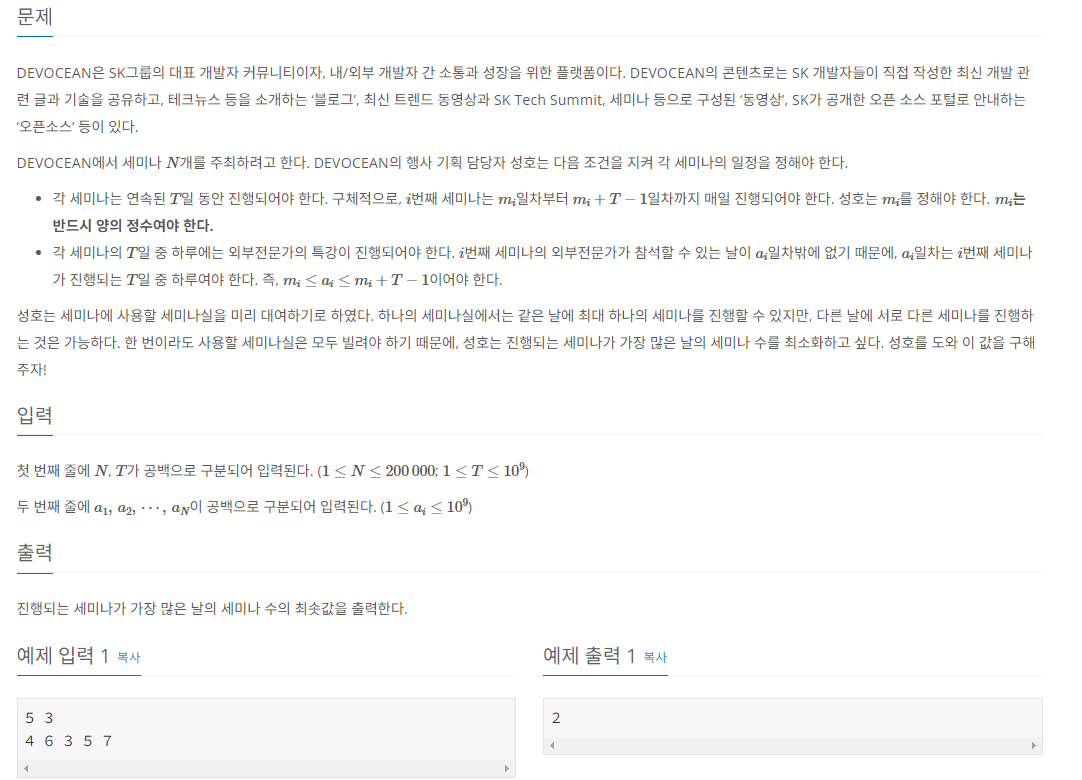

2023 UCPC 예선 K번 문제로, 처음엔 그리디 + 우선순위 큐를 사용하여 시도해 봤지만, 큐가 정렬이 되는 기준을 잡는 것이 힘들었을뿐더러, $a_{i}$값이 중복되는 경우에 항상 답을 도출한다는 보장이 없었다.
해결 방법
답으로 출력될 세미나 수의 최솟값($c$)에 대하여 이분 탐색으로 접근해서 bst 함수에서 그리디하게 $i$번째 세미나의 시작 시간을 정한다. 이때 로직은 $c$가 답으로 도출될 수 있게끔 세미나의 시작 시간을 최대한 빠르게 지정한다 (물론 $a_{i}$가 속하게끔). 이후 모든 세미나의 범위에 $a_{i}$가 속하는지 확인하여 true or false를 반환한다. 반환한 값을 바탕으로 이분 탐색이 끝나면 세미나 수의 최솟값을 구할 수 있으며 이분 탐색 + 그리디로 $O(nlogn)$만에 문제를 해결할 수 있다.
#include<iostream>
#include<algorithm>
using namespace std;
int n, t;
int d[200001], st[200001];
bool bst(int c)
{
for (int i = 1; i <= n; i++) {
if (i <= c) {
st[i] = max(d[i] - t, 1);
}
else {
st[i] = max(d[i] - t, st[i - c] + t);
}
}
for (int i = 1; i <= n; i++) {
if (d[i] < st[i])return false;
}
return true;
}
int main()
{
scanf("%d %d", &n, &t);
for (int i = 1; i <= n; i++) {
scanf("%d", &d[i]);
}
sort(d + 1, d + n + 1);
int st = 1, en = n, mid;
mid = (st + en) / 2;
while (st!=en) {
if (bst(mid)) {
en = mid;
}
else {
st = mid+1;
}
mid = (st + en) / 2;
}
printf("%d\n", mid);
return 0;
}
이분 탐색 / 이진 탐색 (Binary Search)
- 여담으로 이분 탐색과 이진 탐색은 같은 알고리즘을 가리키는 다른 표현으로 같은 용어라 생각하면 된다.
이분 탐색(二分 探索): '이분'이라는 단어는 '둘로 나눈다'는 의미로, 탐색 범위를 반씩 줄여나가는 방식을 의미한다.
이진 탐색(二進 探索): '이진'이라는 단어는 '이진수(0과 1로 이루어진 수)'에서 유래했으며, 역시 탐색 범위를 이진법처럼 두 개로 나누어 탐색하는 방식을 의미한다.