| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 게임 서버 아키텍처
- PROJECT
- 이분 탐색
- ccw 알고리즘
- 비트필드를 이용한 dp
- 최소 공통 조상
- 분리 집합
- map
- 강한 연결 요소
- 벨만-포드
- SCC
- DP
- JavaScript
- Behavior Design Pattern
- Prisma
- Spin Lock
- 트라이
- MongoDB
- 그래프 탐색
- trie
- Strongly Connected Component
- R 그래프
- LCA
- localstorage
- 자바스크립트
- Binary Lifting
- Github
- 2-SAT
- 비트마스킹
- Express.js
- Today
- Total
dh_0e
[Database] DB 설계 이론 본문
Bad Schema

- course 테이블과 department 테이블이 합성된 아주 나쁜 스키마
- deptName을 기준으로 자연 조인 연산을 한 테이블이 나옴

Three anomalies (이상현상)
- Update anomaly
- dept의 정보를 고치려면 n번 고쳐야 함
- ex) 'CS' 학과의 chairman이 바뀌었다면 3번 고쳐야 함
- Delete anomaly
- 수업을 없앴을 때 dept 정보가 모두 날아갈 수 있음
- ex) 222, 223 수업을 삭제하면 'Media' 과의 정보가 날아감
- Insert anomaly
- 새로운 dept 신설 시 과목이 없으면 삽입 불가능
- ex) 'CE' 과가 신설돼도 과목이 없어서 데이터 삽입 불가능

- course 테이블과 room 테이블이 합성된 아주 나쁜 스키마
- course 정보와 room 정보는 전혀 관련이 없기 때문에 두 테이블을 합성하면 카다시안곱이 인스턴스가 됨
- Update anomaly: roomID, building, capacity를 수정할 때 n번 해야 함
- Delete anomaly: cID로 강의를 지우다 보면 room 정보가 날아갈 수 있음
- Insert anomaly: course가 없는 room 정보는 삽입하지도 못함
Design Goal
- 주어진 관계 스키마가 좋은 스키마인지 결정한다.
- 만약 주어진 관계 스키마가 좋지 않은 스키마이면, 주어진 스키마를 다수의 다른 관계로 분해하며,
그 경우 분해된 각 관계 스키마는 좋은 형태이고 또한 분해 과정은 무손실 조인 분해이어야 한다.
Functional Dependencies (함수 종속성)
- 함수 종속성은 유효한 관계 인스턴스에 대한 제약으로, 키 개념의 일반화로 볼 수 있음
- 일부 속성의 값이 다른 속성의 값을 유일하게 결정하는 것을 의미
- t1[a]=t2[a] 이면 t1[B]=t2[b]
- 함수 종속성은 화살표로 나타냄: A → B = "A가 B를 결정한다", "A의 값이 같으면 B의 값도 반드시 같아야 한다"

- A 속성 값이 같은 첫 번째와 두 번째 튜플의 B 속성 값이 동일하며 그 외에는 동일한 속성 값을 가지는 튜플이 없으므로,
A는 B를 함수적으로 결정함 == B는 A에 함수적으로 의존함 - 두 번째와 세 번째 튜플을 보면 B 속성 값이 같으나 A 속성 값이 상이하므로 B는 A를 함수적으로 결정하지 않음
- 함수 종속성은 데이터의 의미나 일관성이 핵심이며 중복 여부는 중요하지 않음
- 모든 A값에 대해 B가 항상 동일한지만 확인하면 OK
Keys
- 만약 a → R이면 a는 슈퍼키
- 슈퍼 키는 관계 속성의 일부분으로서 전체 속성을 함수적으로 결정하는 속성을 의미
- 만약 a → R, !(B ⊂ A, B → R)이면 a는 후보 키
- 만약 a → R이고, B ⊂ A인 어떤 B에 대해서도 B → R이 성립하지 않으면
>> A는 후보 키이다.
- 만약 a → R이고, B ⊂ A인 어떤 B에 대해서도 B → R이 성립하지 않으면
- 후보 키는 슈퍼 키의 성질을 만족하면서, 속성의 서브넷 중 슈퍼 키가 없으면(최소성) 이를 후보 키라고 함
- 후보 키는 모든 속성을 함수적으로 결정하며, 이는 각 속성을 함수적으로 결정
Functional Dependencies의 사용
- 주어진 관계 인스턴스의 유효성을 검사
- 특정 테이블 인스턴스가 주어진 함수 종속성을 만족하여 유효한지 판단 가능
- 적법한 테이블의 제약 조건을 명시하는 데 사용
- 테이블을 설계하고 속성 간의 함수 종속성을 명시하면, 그 테이블 인스턴스는 함수 종속성을 항상 만족해야 함
Functional Dependencies 이론
- 일반적으로 DB 설계자에 의하여 함수 종속성이 결정됨
- 함수 종속성간에 중복성이 존재할 수 있음
- ex) A → C, B → C
- DB 설계 과정에 나쁜 영향을 미치는 함수 종속성이 존재하기도 함
Trivial Functional Dependencies (무의미 함수 종속성)
- B⊆A이면 A → B가 trivial(무의미) : "항상 참이므로 제약 조건으로서 정보가 없음"
- A가 B를 포함하는 슈퍼집합일 때, A가 B를 함수적으로 결정하는 것은 어떤 테이블 인스턴스에 대하여도 항상 만족을 함
- ex) A={학번, 이름}, B={학번} 이면 A → B가 항상 참이기 때문에
"제약 조건으로서의 정보 가치가 없다" = tirival(무의미한)
- ex) A={학번, 이름}, B={학번} 이면 A → B가 항상 참이기 때문에

Closure of a Set of Functional Dependencies (함수 종속성 폐포)
- 함수 종속성은 다른 함수 종속성으로부터 유추할 수가 있음
- ex) A → B, B → C 이면 A → C를 유추할 수 있음
- 어떤 속성 집합 F에 대해, 주어진 함수 종속성 집합 F를 바탕으로 X로부터 함수적으로 유도해 낼 수 있는
모든 속성들의 집합을 $X^{+}$(X의 폐포)라고 함 - 함수 종속성 폐포는 당연히 주어진 함수 종속성을 포함함
- ex) A → B일 때, B⊆A이면 AB → A, ABC → BC 등이 논리적으로 당연히 성립함
Armstrong's Axioms (암스트롱 공리)
- 우주 비행사 닐 팔강해씨가 아니라 캐나다 수학자 암스트롱이 만듦
- 새로운 함수 종속성을 유추할 수 있는 추론 규칙이며 세 가지 추론 규칙으로 구성


- 암스트롱 공리는 sound(건전)하고 complete(완전)함
- sound(건전함)이란 암스트롱 공리를 이용하여 생성되는 모든 함수 종속성은 유효하다는 의미
- complete(완전함)이란 모든 유효한 함수종속성을 암스트롱 공리를 이용하여 생성할 수 있다는 의미
추가 추론 규칙

- union(조합)은 decomposition(분해)과 반대 개념
- pseudotransitivity는 a → b 이고 rb → d 일 때, rb의 b에 a가 들어가서 ra → d가 될 수 있다는 개념

- 위 AG+처럼 주어진 속성의 페포를 구했을 때, 테이블의 전체 속성을 가지게 되면 그 속성은 Super Key
- Super Key가 Candidate Key인 지 확인하기 위해서 각 부분 집합들을 확인해야 함
- AG의 각 부분 집합 A, G가 Super Key 조건이 성립하지 않아야 함 (후보 키는 최소 단위이므로)
Canonical Cover

- 사용자로부터 주어지는 함수 종속성 집합에는 중복되거나 불필요한 속성이 있음
- 이를 찾아 간추리는 게 Canonical cover(정규 커버 또는 최소 커버)
- {A→ B, B → C, A → CD } 예제 - A → CD에서 A → C 및 A → D가 유추됨
>> A → C는 중복적으로 유추가 가능하여 필요 없음, A → D만 남겨도 됨 - {A→ B, B → C, AC → D } 예제 - A → B 및 B → C에서 A → C가 유추되고, - A → C에서 A → AC이므로 A → D가 유추됨
>> AC → D에서 속성 C가 필요 없음

Normal Forms (정규화형)
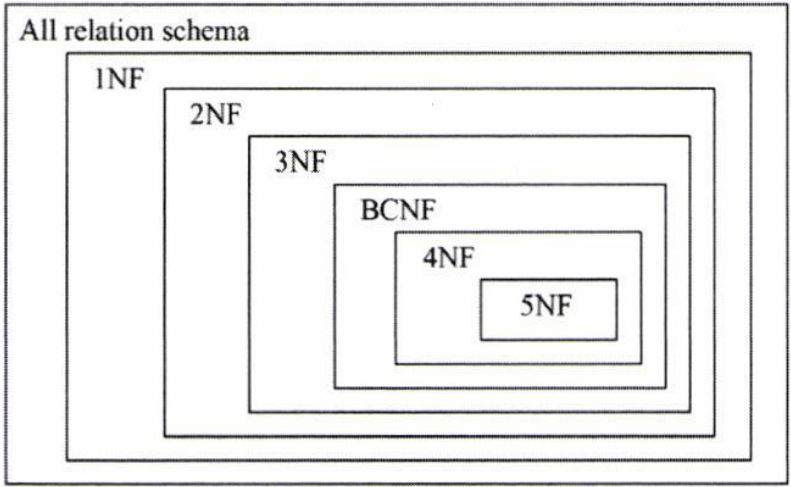
- 관계 정규화에는 총 6개의 정규화형이 있으며 숫자가 커질수록 범위가 좁아짐
- 실질적으로 많이 사용되는 정규형은 제 3 정규형 및 BCNF임
First Normal Form (1NF)
- 제 1정규형은 가장 큰 범위의 정규화형으로 속성 값으로 atomic(원자) 값만을 허용함
- 집합, 리스트(lsit), 백(bag), 복합 속성(compound attribute) 등은 원자 값이 아니므로 허용되지 않음
- 도메인의 모든 값이 원자 값이면 관계형 스키마는 제 1정규화에 속함
다양한 함수 종속성
- 제 2, 3 정규형에서 주로 다룸
Prime, nonprime attribute
- 임의의 후보 키에 속하는 속성은 prime attribute(주요 속성)이라 하며
그렇지 않은 속성은 nonprime attribute(비주요 속성)이라고 함 - 주어진 테이블에 다수 개의 후보 키가 존재하는 경우, 최소한 하나 후보 키에 속해도 주요 속성이 됨
- ex) 테이블 R(StudentID, CourseID, Grade)에서
Prime attribute: StudentID, CourseID
Nonprime attribute: Grade
- ex) 테이블 R(StudentID, CourseID, Grade)에서
Functional dependency
Full functional dependency (완전 함수 종속성)
- 함수 종속성 "a → b"에서 a의 모든 부분 집합이 r이라 했을 때, "r → b"가 성립하는 부분 집합이 하나도 없을 때를 의미
- ex) ar → b일 때, a → b, r → b가 둘 다 성립하지 않아야만 ar = fully dependent
- 단일 기본키: Dependent가 기본키(key 하나)에만 종속되는 경우
→ "학번(pk) / 이름, 학년, 성별, 학과명"으로 구성된 테이블에서 학번 필드가 이름, 학년, 성별, 학과명을 모두 결정하기
때문에 이를 완전 함수 종속 관계라고 말한다. - 복합 기본키: Dependent가 기본키를 구성하는 모든 속성에 대해 종속되는 경우
→ "학번(pk), 과목번호(pk) / 성적"으로 구성된 테이블에서 학번, 과목번호 필드가 성적을 결정하고,
학번 또는 과목번호만으로는 성적을 결정할 수 없기 때문에 이를 완전 함수 종속 관계라고 말한다. - 출처: https://velog.io/@gmlstjq123/10%EC%A3%BC%EC%B0%A8-%EC%9D%B4%EB%A1%A0.-Functional-Dependencies-and-Normalization
- 단일 기본키: Dependent가 기본키(key 하나)에만 종속되는 경우
Partial functional dependency (부분 함수 종속성)
- Partial 함수 종속성 기준
"a → b"에서 a의 부분 집합 r만 가지고도 b를 결정할 수 있는 경우 - ex) ar → b일 때, a → b 이면 ar = partial dependent
- 단일 기본키 (후보 키가 단일일 경우) : 부분 함수 종속이 발생하지 않음
- 복합 기본키: 기본키를 구성하는 속성 중 일부에만 종속되는 경우
→ "학번(pk), 과목번호(pk) / 학년, 성적"으로 구성된 테이블에서 학년은 학번에만 종속되기 때문에 이를 partial 함수 종속 관계라고 한다. (이때, 성적은 완전 함수 종속 관계가 됨)- 출처:
Transitive functional dependency (이행 함수 종속성)
- 암스트롱 공리의 Transitivity Rule(이행규칙)을 이용하여 생성되는 함수 종속성을 의미
- ex) "a → b", "b → r" 일 때, a → r은 transitivity dependent
Second Normal Form (2NF)
2NF 기준
- 후보키의 진부분집합(자기 자신을 제외한 부분집합)이 non-prime attribute(비주류 속성)를 결정하지 않아야 함
"후보키의 전체를 쓰지 않고 일부만으로 결정된 포함관계가 있느냐"가 기준
- ex) R(A, B, C)에서 AB가 후보 키이며 AB → C일 때,
A → C가 성립한다면, A가 후보키 AB의 진부분집합이며 C가 nonprime 속성이므로
Partial dependent가 발생하여 2NF가 될 수 없음
- ex) R(A, B, C)에서 AB가 후보 키이며 AB → C일 때,
- ※ 하지만 만약 C가 prime attribute(후보 키에 포함된 속성)이라면,
partial dependency는 발생하지만 이는 2NF를 위반하지 않음
- ex) AC가 후보 키이며 A → C라면 A가 후보키 AC의 진부분집합이지만 C가 prime 속성이라 괜찮음 >> 2NF 가능
- ex) AC가 후보 키이며 A → C라면 A가 후보키 AC의 진부분집합이지만 C가 prime 속성이라 괜찮음 >> 2NF 가능
- 즉, Partial Dependency(부분 종속)이 없으면 2NF를 만족함
- ex) 학생(학번, 과목번호, 성적, 나이) 테이블에서 기본키가 (학번, 과목번호) 일 때,
나이는 학번에만 종속되므로 후보 키 전체에 대해 partial dependency가 발생하여 2NF 조건을 만족하지 못함
>> 따라서 나이를 별도 테이블(학번, 나이)로 분리하면 2NF를 만족하게 됨
- ex) 학생(학번, 과목번호, 성적, 나이) 테이블에서 기본키가 (학번, 과목번호) 일 때,

- hours를 제외한 비주요속성인 eName, pName, pLocation 모두 후보 키 (SSN, pNumber)에 부분적으로 의존함
동시에 후보 키의 진부분집합에 종속됨 (SSN → eName, pNumber → pName, pLocation)
>> 2NF 조건 충족 X - R1, R2, R3로 나눠서 각자 의존하던 "후보 키의 부분 집합"을 후보 키로 삼고 테이블을 이루면 2NF 만족

- 비주요 속성인 Status, City가 후보 키의 부분 집합인 S#에 의존하므로 2NF가 될 수 없음
- SECOND, SP로 테이블을 분해하면 두 테이블 모두 비주요 속성이 후보 키에 완전 의존되므로 2NF가 만족함
- 하지만, 비주요 속성인 City가 Status를 포함하기 때문에 3NF가 될 수는 없음 // 3NF 조건
- S# → City, Status라는 부분 함수 종속이
S#, P# → City, Status보다 정규화 기준에서는 우선적으로 고려하여 테이블 분해한 것

- 이런 경우 또한, D를 결정하는 함수 종속성이 없으므로 후보 키에 포함되어야 하며, 후보 키는 A, D가 됨
- B, C가 후보 키의 부분 집합인 A에 종속되고 있으므로 partial dependency 발생으로 2NF 조건 위반 >> 1NF임
Third Normal Form (3NF)
- 제 2정규형 중에서 nonprime attribute(비주요 속성)이 후보 키 전체에 transitively(이행적)으로 의존적이 아니면 제 3 정규형임
- 즉, 어떤 함수 종속 X → A가 있을 때, 3NF를 만족하려면 다음 중 하나 이상이면 된다
- 가 후보 키 전체일 경우
-
- ex) R(A, B, C, D)에서 (A, B)가 후보 키일 때, ABC → A인 경우
ABC가 후보 키는 아니지만, A가 ABC의 부분 집합임은 자명한 것
- ex) R(A, B, C, D)에서 (A, B)가 후보 키일 때, ABC → A인 경우
- 가 주요 속성 (Prime Attribute) 일 경우
- ex) R(A, B, C, D)의 후보 키가 (A, B) 일 때, C → A일 경우
애초에 (A, B)가 후보 키라는 것은 C 때문에 A가 정해지는 것은 아니기 때문에 성립 - 이 조건이 사라지면 BCNF의 조건이 되는 것
- ex) R(A, B, C, D)의 후보 키가 (A, B) 일 때, C → A일 경우


BCNF (Boyce/Codd Normal Form)
- 관계형 스키마의 모든 함수 종속성 "X → A"에서 X가 슈퍼 키이면 BCNF 정규형
- 모든 슈퍼 키는 적어도 하나의 후보 키를 포함하고 있으므로,
결정자 X가 슈퍼 키라면 → 그 튜플은 절대 중복되지 않음 >> 안정된 구조 보장
- 모든 슈퍼 키는 적어도 하나의 후보 키를 포함하고 있으므로,
- 제 3정규형의 정의에서 3번째 조건인 "a → b에서 a가 nonprime attribute일 때, b가 prime attribute인 조건"을 삭제한 것

- MovieStudio에서 studioName이 후보 키가 아니며(3NF의 1조건 위배), Trivial 아님(2조건 위배),
그렇다고 studioAddr이 prime attribute도 아님(3조건 위배) >> 3NF 아님 - 하지만 Partial dependency(부분 종속)이 발생하지 않고 있으므로 2NF라고 할 수 있음
속성이 2개인 테이블은 모두가 BCNF임

- 속성들 간 trivial(무의미한, 자명한) 종속이 없으면 전체가 key라는 말은
“속성들 간에 자명한 종속 외에는 아무런 함수 종속이 없다면, 릴레이션의 전체 속성 집합이 후보 키다” 이 말임 잘못 필기함- R(A, B, C) 에서 함수 종속이 아무것도 없거나 A → A, AB → A 등 trivial 한 것만 있다면
>> A, B, C 중 어떤 하나로도 다른 속성을 결정 못함
>> 전체 속성 집합인 (A, B, C)가 후보 키임
- R(A, B, C) 에서 함수 종속이 아무것도 없거나 A → A, AB → A 등 trivial 한 것만 있다면
- 요딴 Schema는 A, B, C, D 모두 각자의 폐포가 모든 속성임
>> 후보 키는 A, B, C, D 모두 (후보 키가 여러 개임)
>> E만 non-prime이며 BCNF까지 만족함 - ※ 추가적으로, 위 예시에 나온 것처럼 (A, B) 속성이 2개뿐인 테이블은 BCNF를 자동으로 만족함
Practice
- 스키마와 관련 함수 종속성이 주어지고 주어진 스카마에 대한 정규형을 결정하는 문제
- 순서: 모든 후보 키를 구하고, 주요 속성과 비주요 속성을 구한 뒤, 주어진 스키마에 대한 정규형을 판별

- 속성 C, D, E, F 모두 후보 키(A, B)의 부분 집합에 의존하고 있는 함수 종속성
- 속성 A, C, D와 B, E, F는 전혀 관련이 없는 아주 좋지 않은 스키마
- Partial dependency가 존재하기 때문에 2NF를 만족하지 못함 >> 1NF

- Partial dependency가 없으므로 2NF 만족
- C → D는 nonprime이 nonprime을 결정하고 있으므로 3NF 조건 X
- R1(A, B, C, E), R2(C, D)로 분리하면 BCNF 만족

- 마찬가지로 Partial dependency는 없는데 non to non이 존재하므로 2NF
- R1(A, B, C) R2(C, D, E)로 분리하면 BCNF 만족
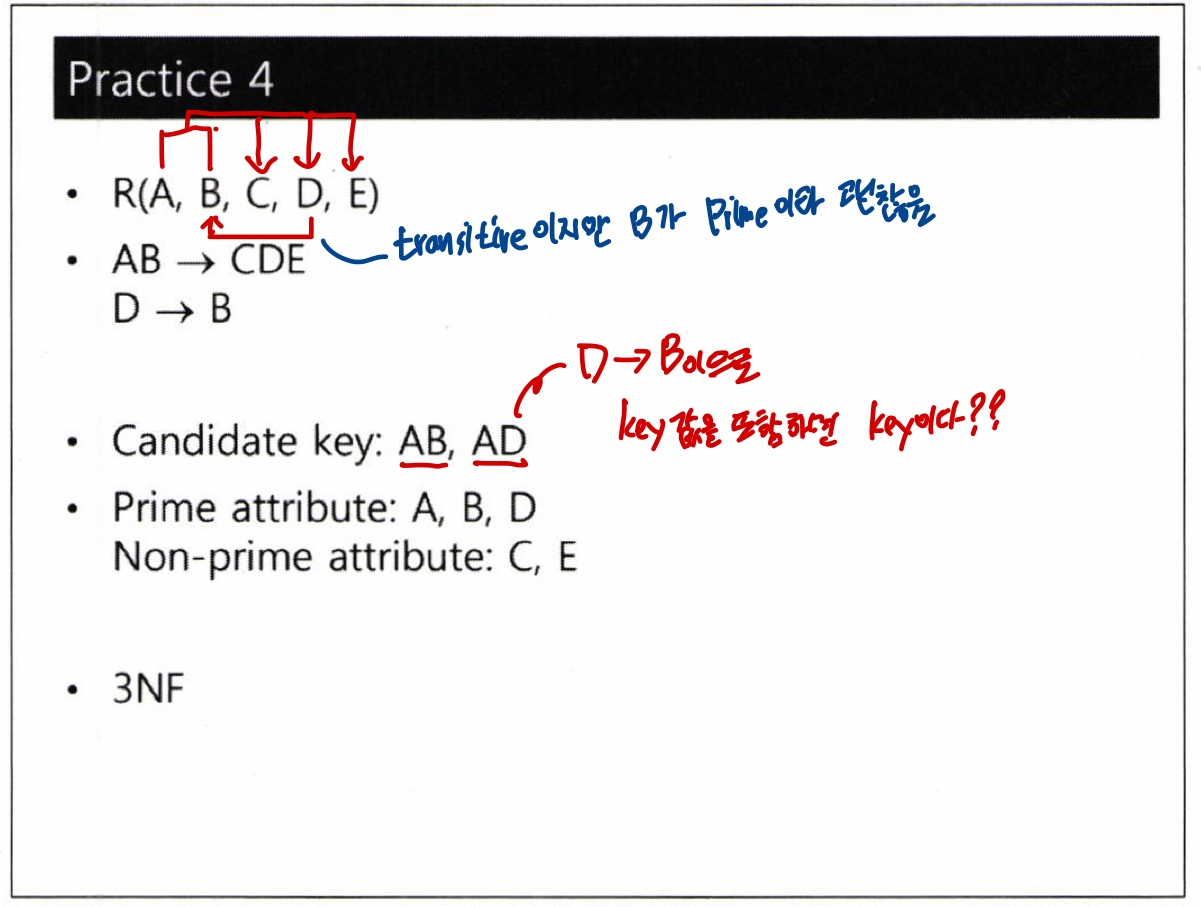
- 3NF의 3조건(비주요 속성이 주요 속성을 포함)을 만족하기 때문에 3NF 가능
- 하지만 3NF의 3조건을 만족하면 BCNF가 될 수 없음
- AB → CDE로 AB는 슈퍼키 조건을 만족하지만,
D → B는 A를 결정하지 못하기 때문에 D는 슈퍼키가 아니므로 BCNF 위반
- AB → CDE로 AB는 슈퍼키 조건을 만족하지만,
필기에 물음표는 느낌표임
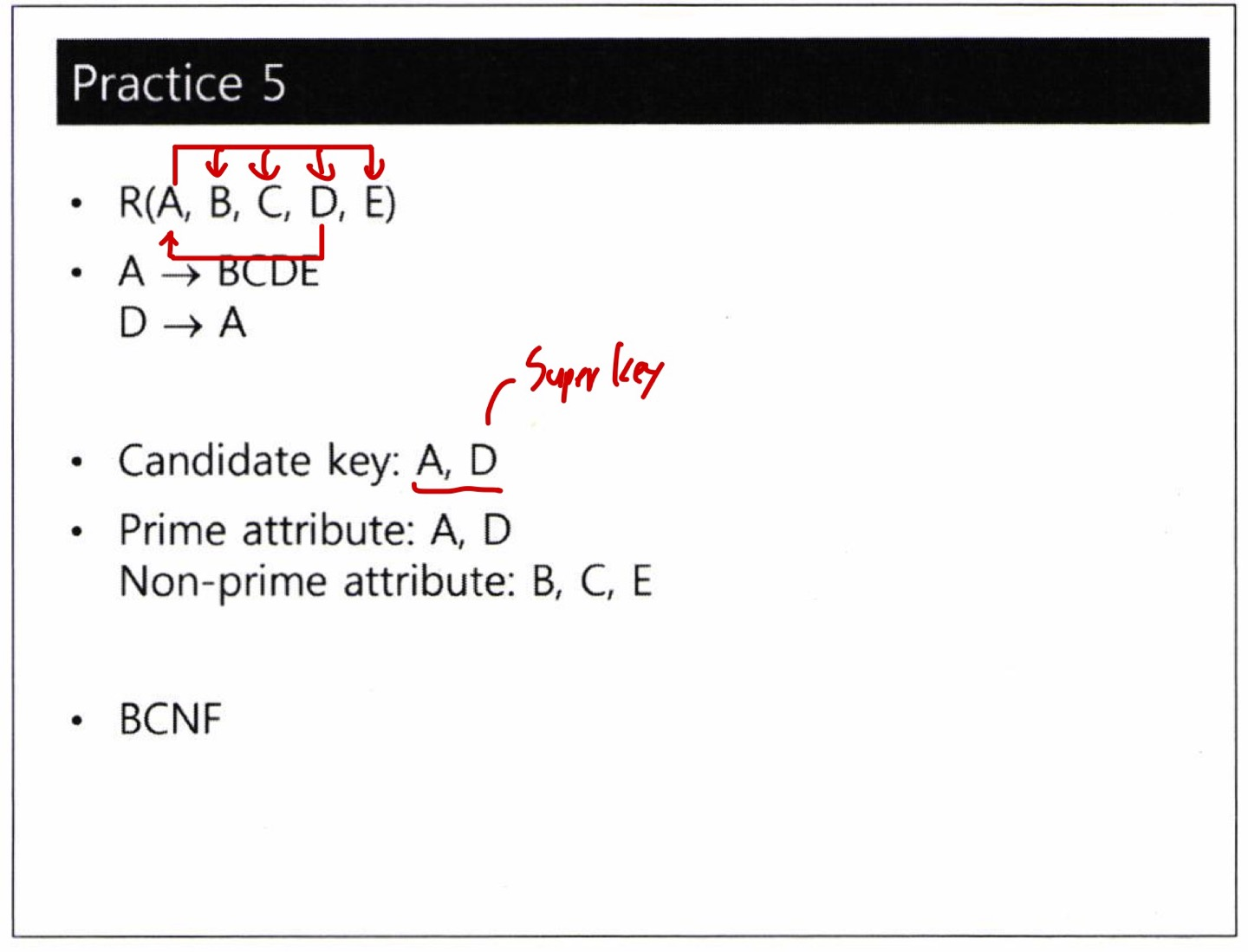
- 마찬가지지만 A, D 모두 슈퍼 키이므로 BCNF 성립

- 아주 좋아요

- 아까 나왔던 "요딴 스키마"랑 비슷한 구조
- A, B, C, D 모두 하나만 있어도 모든 속성을 결정할 수 있으므로 모두 후보 키
- 정의에 A, B, C, D 모두 슈퍼 키이므로 BCNF 성립
정규화 목표
- 함수 종속성을 이용하는 정규화의 목표는 주어진 스키가 좋은 스키마인지 결정하는 것
- 주어진 스키마가 좋은 스키마가 아니라면 분해(decompose)를 통해 다수 개의 작은 관계형 스키마로 변형
- 생성된 작은 스키마들은 모두 좋은 스키마(3NF, BCNF)여야 하며 lossless join decomposition(무손실 조인 분해)여야 함
- 또한 함수 종속성을 보존(dependency preserving)하는 분해이면 더 좋음
무손실 조인 분해

- 위 과정은 무손실 조인분해의 반대 분해인 손실 조인 분해(lossy join decomposition)의 예시
- 다음과 같이 분해된 employee 테이블을 다시 생성하기 위해 자연 조인을 실행하면 없던 튜플이 생성됨
- 2, 4번째 행은 원래 테이블에는 없던 튜플이며 분해 및 조인 연산 과정에서 부가적으로 생성된 튜플임
- 이를 spurious 튜플이라 함
- 무손실 조인 분해를 하면, 분해된 테이블에 대하여 자연 조인 연산을 한 결과가 원래 테이블과 동일해야 함

무손실 조인 분해의 조건
- 분해된 테이블의 공통 속성이 분해된 테이블 중 적어도 하나에서 주 키이어야 함
- 주 키는 여러 개의 후보 키 중 사용자가 선택한 하나의 대표 키
- 즉, 위 필기 예시에서 R 테이블을 R1, R2로 분해했을 때, "R1∩R2"가 R1 or R2의 주 키이면 무손실 조인 분해가 성립
- 다른 말로, 테이블 R이 R1, R2, ..., Rn으로 분해되는 경우
R의 함수 종속성 F의 폐포가 모든 테이블을 조인했을 때의 폐포와 같거나 이를 포함해야 함

- 위 예시에는 함수 종속성이 나오지 않았으므로 아래 예시를 살펴보자

- 다음 예시에선 F1의 함수 종속성과 F2의 함수 종속성을 union하여 폐포를 구한 것이 원래 테이블의 폐포와 똑같음
F1={A → B}, F2={B → C}이며 (F1 U F2)+ == F+ 이므로 무손실 조인 분해 & 함수 종속성 보존
- 그 아래의 반례에선 F1 U F2의 폐포가 {A → B}밖에 없어서 원래 함수의 폐포 {A → B, B → C, A → C}와 다르기 때문에 함수 종속성 보존이 불가능함
F1={A → B}, F2={}이며 (F1 U F2)+ != F+ 이므로 무손실 조인 분해 & 함수 종속성 미보존

- 다음 예시에서 E는 함수 종속성이 없으므로 반드시 후보 키에 포함되어, 후보 키는 ACE가 됨
- 테이블 R은 E를 포함하는 함수 종속성이 없기 때문에, partial dependency가 발생해서 제2정규화 조건 만족 X >> 1NF
- AC → D를 유도하면 후보 키 ACE의 진부분집합인 AC에 D가 의존하므로 partial dependency 발생
- 이를 AC → D를 근거로 R1과 R2로 분해하면 함수 종속성이 보존됨
- F₁ = {A → B}, F₂ = {AC → D}로 분해했을 때,
이 둘을 합한 종속성 집합의 폐포가 원래의 F⁺(A → B, BC → D 등)를 포함
>> 함수 종속성 보존 조건을 만족 - R₁은 A → B가 존재하고, A가 슈퍼 키이므로 BCNF를 만족
- R2는 후보 키가 ACE이며, 비주요 속성인 D가 후보 키의 부분 집합 AC에 포함되므로
partial dependency 발생 >> 1NF
- F₁ = {A → B}, F₂ = {AC → D}로 분해했을 때,
BCNF Decomposition
- 정규화되지 않은 R을 BCNF를 만족하는 여러 개의 하위 relation으로 분해하는 과정
- Lossless-join decomposition(무손실 조인 분해)을 반드시 보장해야 하며,
가능하면 Dependency Preserving(함수 종속 보존)도 함께 만족하는 것이 이상적임

- B → C는 nonprime → nonprime이므로 3NF 조건 위반
- 후보 키 A에 대하여 partial dependency가 발생할 수 없으므로 2NF 조건 만족
- 분해된 테이블 R1, R2는 속성 2개인 테이블이므로 BCNF 만족 / 하지만 함수 종속성 보존되지 않음
- 다음과 같은 스키마는 "BCNF로 분해할 수 있다고, 항상 함수 종속성 보존을 만족하지는 않는다"를 보여주는 반례임
- 위 스키마는 그냥 함수 종속성을 보존하면서 분해할 수 있는 방법이 없는 스키마임
- ※ 하지만 3NF로의 무손실 조인 분해는 항상 함수 종속성을 보존할 수 있음
- 사실 1NF, 2NF의 정의를 만들고 아 이제 좋은 스키마를 BCNF로 정의하고 끝내자! 했는데
BCNF는 정규화 이상을 완전히 제거하지만, 항상 함수 종속성을 보존하지 못하는 문제점 발생
>> FD 보존과 무손실 조인을 모두 만족하는 3NF가 도입된 것
- 사실 1NF, 2NF의 정의를 만들고 아 이제 좋은 스키마를 BCNF로 정의하고 끝내자! 했는데
But 3NF에선 중복이 존재

- 위에서 본 3NF 예제를 다시 한번 보면, L → K에서 L이 후보 키가 아니지만, K가 Prime attribute 이므로 3NF 조건을 만족
- 이런 경우 l1, k1 처럼 인스턴스의 중복이 발생할 수 있으며,
이로 인하여 세 가지 이상(저 위에서 설명한 Update, Delete, Insert anomalies)이 발생할 수 있음
3NF 판별 및 분해
- 이러한 이유로 3NF인지 판별하는 과정은 NP-hard(겁나 어렵고 오래 걸림)인데, 3NF로 분해하는 과정은 polynomial time(다항 시간)에 수행할 수 있음(꽤 빠름)
- 실무에선 판단보다는 바로 분해하는 방식을 자주 씀
- 3NF를 판별할 땐, F에 있는 함수 종속성만 보면 됨 (F+를 안 봐도 됨)
- A → B가 있을 때:
- A가 슈퍼 키면 OK
- 아니면, B가 전부 후보 키에 포함된 속성(prime attribute)이면 OK
결론

- 추구하는 이상 스키마는 BCNF, 무손실 조인 가능, 함수 종속성 보존이지만,
함수 종속성 보존이 중요한 응용에서는 3NF를 사용해도 됨- 실무에서 3NF, BCNF가 가장 널리 사용됨
'Database' 카테고리의 다른 글
| [Database] Entity-Relationship Data Model (0) | 2025.06.02 |
|---|---|
| [Database] SQL 확장 (1) | 2025.05.21 |
| [Database] 응용 개발 (0) | 2025.05.20 |
| [Database] 오라클 실습 II (0) | 2025.05.20 |
| [Database] 데이터베이스 시스템 주요 기능 (0) | 2025.05.19 |




