| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 2-SAT
- Github
- 게임 서버 아키텍처
- localstorage
- map
- Prisma
- 이분 탐색
- Spin Lock
- Behavior Design Pattern
- DP
- 그래프 탐색
- trie
- PROJECT
- 비트필드를 이용한 dp
- SCC
- 분리 집합
- Express.js
- 비트마스킹
- LCA
- Strongly Connected Component
- 강한 연결 요소
- 최소 공통 조상
- 벨만-포드
- JavaScript
- 트라이
- ccw 알고리즘
- MongoDB
- 자바스크립트
- R 그래프
- Binary Lifting
Archives
- Today
- Total
dh_0e
[C++] 행렬 곱셈(matrix multiplication) 정의와 그 이유, 구현 본문
행렬의 곱셈
조건
- m x n 행렬 A와 i x j 행려 B가 존재할 때, 행렬 A의 열 크기(n)와 행렬 B의 행 크기(i)가 같아야만 행렬의 곱셈이 가능
정의
- 두 행렬 A와 B가 있을 때, 이 둘의 곱 C=A⋅B는 다음과 같이 정의됨


- 다음과 같은 2x3 행렬 A와 3x2 행렬 B가 있을 때, 행렬 A의 열 크기(3)와 행렬 B의 행 크기(3)가 같으므로 행렬의 곱이 가능
- C=A⋅B일 때, C는 2x2 행렬이며 각 요소는 다음과 같이 계산됨
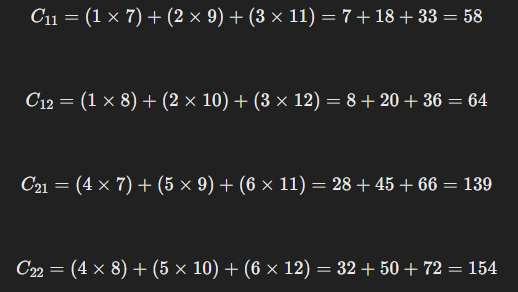

행렬의 곱을 이렇게 정의하는 이유
선형변환(Linear Transformation)
- 선형적(직선으로) 변화하는 것
- 선형 변환은 벡터 공간에서 벡터를 다른 벡터로 매핑하는 함수
행렬은 벡터를 다른 벡터로 변환하는 일종의 도구이며 이는 선형 변환을 나타낼 수 있다는 뜻이며, 다음 예와 같이 행렬의 곱셈으로 쉽게 구성할 수 있음
선형변환 T에 대해 T(x) = Ax인 행렬 A가 있고, 선형변환 L(x) = Bx 일 때,
(LºT)(x) = BAx 임이 증명되어 있음
C++ 구현
이를 C++로 구현하면 다음과 같다
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> solution(vector<vector<int>> A, vector<vector<int>> B) {
vector<vector<int>> C;
int A_row = A.size(), A_column = A[0].size(), B_row = B.size(), B_column = B[0].size();
if (A_column != B_row) {
cout << "Can't multiply the matrices." << endl;
return {};
}
for (int i = 0; i < A_row; i++) {
vector<int> vec;
for (int j = 0; j < B_column; j++) {
int c = 0;
for (int k = 0; k < A_column; k++) {
c += A[i][k] * B[k][j];
}
vec.push_back(c);
}
C.push_back(vec);
}
return C;
}
int main() {
vector<vector<int>> A = {
{1, 2, 3},
{4, 5, 6}
};
vector<vector<int>> B = {
{7, 8},
{9, 10},
{11, 12}
};
vector<vector<int>> C = solution(A, B);
cout << "C:" << endl;
for (const auto& row : C) {
for (int val : row) {
cout << val << " ";
}
cout << endl;
}
return 0;
}'C++' 카테고리의 다른 글
| [C++] memset, isupper/islower (0) | 2025.02.13 |
|---|---|
| [C++] stringstream (2) | 2024.07.22 |
| [C++] max_element, min_element, find (0) | 2024.07.12 |
| [C++] map, unordered_map (0) | 2024.07.03 |
| [C++] stoi/stol/stoll, <string> method (0) | 2024.06.24 |




